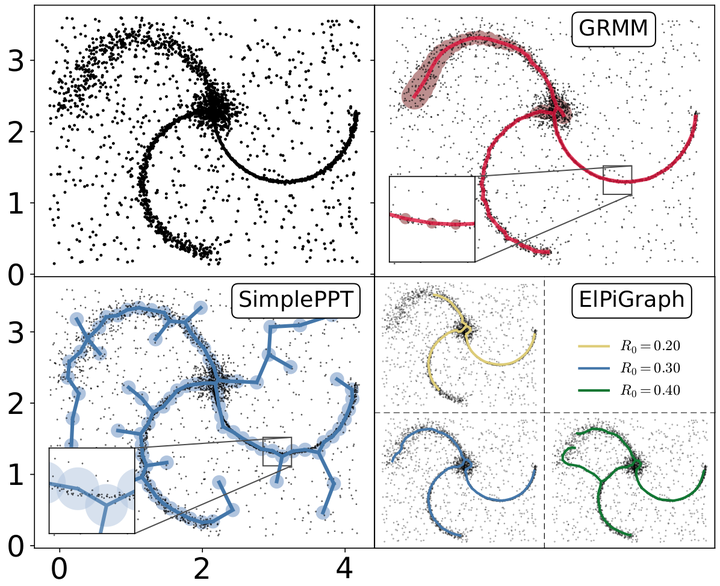
Comparison of several algorithms to identify a principal graph in point-cloud datasets.
Abstract
A regularized version of Mixture Models is proposed to learn a principal graph from a distribution of D-dimensional data points. In the particular case of manifold learning for ridge detection, we assume that the underlying manifold can be modeled as a graph structure acting like a topological prior for the Gaussian clusters turning the problem into a maximum a posteriori estimation. Parameters of the model are iteratively estimated through an Expectation-Maximization procedure making the learning of the structure computationally efficient with guaranteed convergence for any graph prior in a polynomial time. We also embed in the formalism a natural way to make the algorithm robust to outliers of the pattern and heteroscedasticity of the manifold sampling coherently with the graph structure. The method uses a graph prior given by the minimum spanning tree that we extend using random sub-samplings of the dataset to take into account cycles that can be observed in the spatial distribution.
