About me
I graduated from the french engineering school CentraleSupélec with a major background in applied mathematics and algorithmic. After a year of working as a research engineer in Thales, I decided to begin a Ph.D. program in Université Paris Saclay, at the Institut d'Astrophysique Spatiale, under the supervision of Nabila Aghanim (IAS) and Aurélien Decelle (UCM, LRI).
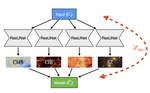
I am currently a postdoctoral researcher at the École Normale Supérieure (ENS) in Paris working on the interfaces between statistical physics and machine learning algorithms in Giulio Biroli's team at the center for data sciences.
- Interfaces physics/machine learning
- Algorithmics & Machine Learning
- Cosmology: Large-scale structures of the Universe
-
Ph.D. in Astrophysics & Cosmology, 2021
Université Paris-Saclay
-
Engineering school, 2017
CentraleSupélec
Experience
AI for physics and physics for AI: development of AI-based tools for astrophysics and cosmology and exploration of the links between theoretical physics and AI for a better understanding of AI systems. Teaching duty under the data science program of PSL University.
Applying statistical physics models for the understanding of machine learning algorithms.
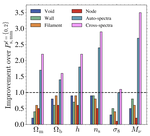
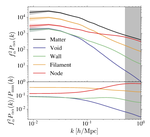
Cosmic web environments: identification, characterisation and quantification of cosmological information.
Conception and development of unsupervised algorithms to deinterleave radar pulses collected by satellites.
Publications
Recent & Upcoming Talks
Contact
- bonnaire.tony@gmail.com
- 45 rue d'Ulm, Paris, 75005
- Staircase B, 3rd floor